重要な性質３

転置行列には面白い性質があり、ゲームではこれが良く使われています。
面白い性質というのは以下のとおりです。

つまり、計算の順番を入れ替える事ができる訳です。

---

ＤｉｒｅｃｔＸ８．０ではこの性質を使って座標変換を判りやすくプログラミング
できるようにしています。

（筆者駐：わざわざ判りにくく書かなければいけないようにしてあるとも言える。)

例えば、敵キャラなどの３Ｄオブジェクトを回転させてから移動させるには、
以下の様に計算するのですが、

移動 マトリクス

回転 マトリクス

頂点 座標

これを敵キャラのデータのポリゴンの頂点毎に計算する事になる訳です。

という事は敵キャラの頂点毎に、行列の積を２回計算する事になりますが。
結合法則を使うと、１回にまとめる事ができるので、

高速化の為、結合法則を使って以下の様に書き換えます。

移動 マトリクス

回転 マトリクス

頂点 座標

この、

移動 マトリクス

回転 マトリクス

の部分を、別に計算しておいて、ワールドマトリックスなるものを作っておきます。
んでもって、

ワールド マトリクス

頂点 座標

という風に計算する訳です。

ただ、回転させて移動させるのに、移動×回転という順番がわかりにくいからか、
ＤｉｒｅｃｔＸ８．０では、以下の様にワールドマトリックスを算出しています。
（本当の理由は良くわからない、かえって混乱をまねいているような気がする。）

ｔ 回転 マトリクス

ｔ 移動 マトリクス

ほんでもってポリゴンを座標変換して表示する時に、
こんな風に計算する訳です。

ｔ ワールド マトリクス

頂点 座標

そんな訳で、以下の関数は、それぞれ以下の表のような出力をします。
（同様の機能を持つ他の関数も同じです。）

関数名	出力
D3DXMatrixRotationX	ｔ Ｘ軸回転 マトリクス
D3DXMatrixRotationY	ｔ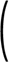 Ｙ軸回転 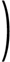マトリクス
D3DXMatrixRotationZ	ｔ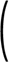 Ｚ軸回転 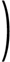マトリクス
D3DXMatrixTranslation	ｔ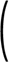 移動 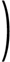マトリクス
D3DXMatrixTranslation	ｔ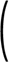 スケーリング 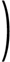マトリクス

行列の話題はこのへんで終わります。プログラム演習課題へ戻る