行列の積についての重要な性質


下の表の中のＡ，ＢおよびＣはいずれも行列であるものとします。
この時、以下の法則のそれぞれは、下の表のようになります。

交換法則は×ＡＢ≠ＢＡ
結合法則は○（ＡＢ）Ｃ＝Ａ（ＢＣ）
分配法則は○Ａ（Ｂ＋Ｃ）＝ＡＢ＋ＡＣ



試してみましょう。
まずは交換法則から。

【交換法則】　ＡＢ≠ＢＡ

3 1
6 7
2 5
4 9
＝
10 24
40 93

2 5
4 9
3 1
6 7
＝
36 37
66 67

掛け算の順番を入れ替えただけなのに、まったく答えが変わるのが判ります。

【結合法則】　（ＡＢ）Ｃ＝Ａ（ＢＣ）

2 5
4 9
3 1
6 7
8 -4
-5 7
＝
36 37
66 67
8 -4
-5 7
＝
103 115
193 205

2 5
4 9
3 1
6 7
8 -4
-5 7
＝
2 5
4 9
19 -5
13 25
＝
103 115
193 205

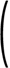
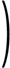
これでは法則の証明にまでは到りませんが、実際このようになります。

【分配法則】　Ａ（Ｂ＋Ｃ）＝ＡＢ＋ＡＣ

2 5
4 9
3 1
6 7
＋
8 -4
-5 7
＝
2 5
4 9
11 -3
1 14
＝
27 64
53 114

2 5
4 9
3 1
6 7
＋
2 5
4 9
8 -4
-5 7
＝
36 37
66 67
＋
-9 27
-13 47
＝
27 64
53 114

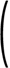
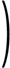
これも法則の証明には到りませんが、実際法則どおりになる事が判ります。



もう少し行列の性質を見てみましょう。 次のページ